Poliedros Convexos

Uma superfície poliédrica limitada convexa é a união de um número finito de polígonos planos e convexos, tais que:

(i) 2 polígonos não estão no mesmo plano;

(ii) Cada lado de polígono não está em mais que 2 polígonos;

(iii) Havendo lados de polígonos que estão em 1 só polígono, eles devem formar uma única poligonal fechada, plana ou não, chamada contorno;

(iv) O plano de cada polígono deixa os demais num mesmo semi-espaço.

 

As superfícies poliédricas limitadas convexas que têm contorno são chamadas abertas. As que não têm contorno são chamadas fechadas.

 

Elementos:

 

Uma superfície poliédrica limitada convexa possui:

Faces: são os polígonos;

Arestas: são os lados dos polígonos;

Vértices: são os vértices dos polígonos;

Ângulos: são os ângulos dos polígonos.

 

Poliedro Convexo:

 

Consideremos um número finito n, maior ou igual a 4, de polígonos planos convexos tais que:

(i) dois polígonos não estão num mesmo plano;

(ii)  cada lado de polígono é comum a dois e somente dois polígonos;

(iii) o plano de cada polígono deixa os demais polígonos num mesmo semi-espaço.

 

Nessas condições, ficam determinados n semi-espaços, cada um dos quais tem origem no plano de um polígono e contém os restantes. A interseção desses semi-espaços é chamado Poliedro Convexo.

 

Para todo Poliedro Convexo, ou para a sua superfície, vale a Relação de Euler:  

      V + F = A + 2

onde V é o número de vértices do poliedro, F é o número de faces e A é o número de arestas.

 

Soma dos ângulos de todas as faces de um poliedro:

S = 360 (V - 2)

onde V é o número de vértices do poliedro.

 

Relação entre faces e arestas:

3F₃  + 4F₄ + 5F₅ + ... = 2A

 

Cálculo do número de diagonais de um poliedro:

d = C_V,2 - A -  S_dF

onde A é o número de arestas do poliedro, C_V,2 é a combinação do número de vértices tomados 2 a 2 e S_dF é o somatório do número de diagonais das faces do poliedro.

 

Poliedros Regulares:

 

Todo Poliedro Regular é Poliedro de Platão.

 

Existem 5 tipos de poliedros regulares : Tetraedro, Hexaedro, Octaedro, Dodecaedro e Icosaedro.

 

 

 

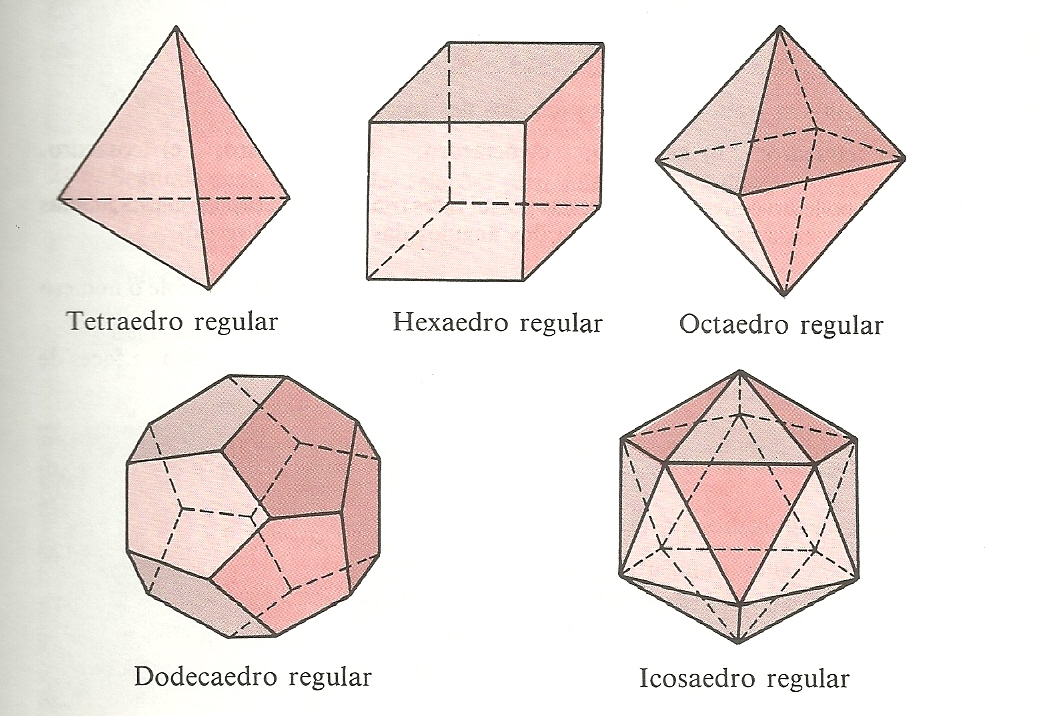
(Fonte: Fundamentos de Matemática Elementar, Volume 10, Gelson Iezzi - Geometria Espacial.)

 

Lista de Exercícios: 

 

Lista 1:  (Poliedros convexos e relação de Euler)